感觉这场自己发挥得还可以,切掉了 $1003、1004、1006$,队友开局秒切博弈,然后我也过了道签到,然后来到了赛中最高排名,好像是 $rk 30+$。
但是过掉 $1006$ 后发现 $1002$ 居然已经过了一百多个队,但是已经没时间了,而且大家都不想写了,心有余而力不足吧,最终 $rk207$。
对了,今天我换了一种代码风格,开始使用std::码风,感觉又变快乐了。
1002-Independent Feedback Vertex Set
题目描述
给你一个由三元环组成的图,每个点都有一个权值。你可以选择一些点,并且选择的点两两之间没有直接相连的边,最大化选择点的点权和。
思路
???题目一解读完感觉就是道水题,难怪最后过了这么多,只能怪在 $1006$ 耗太多时间了。
由于只含有三元环,我们对每个点染色,来张图感性地认识一下。
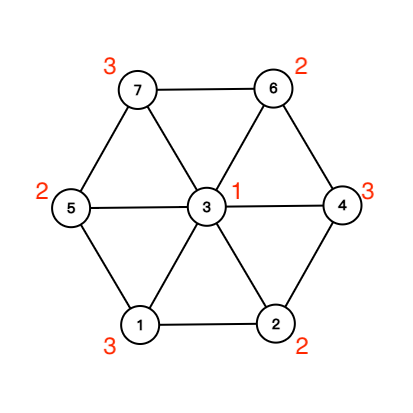
若选择 $3$ ,我们发现没有别的点可选。
若选择 $1$ ,我们可以选择同为标上 $3$ 的 $7,4$。
若选择 $2$ ,我们可以选择同为标上 $2$ 的 $5,6$。
我们发现我们的选择只有三种,即三种颜色的节点集,最后计算每个颜色集的权值和,取最大值即可。
代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
| #include<bits/stdc++.h>
using LL = long long;
void solve() {
int n;
std::cin >> n;
std::vector< int > v(n), c(n);
for (int i = 0; i < n; ++ i) {
std::cin >> v[i];
}
c[0] = 0;
c[1] = 1;
c[2] = 2;
for (int i = 3; i < n; ++ i) {
int u, v;
std::cin >> u >> v;
-- u;
-- v;
c[i] = 3 - c[u] - c[v];
}
std::vector< LL > mx(3);
for (int i = 0; i < n; ++ i) {
mx[c[i]] += v[i];
}
std::cout << std::max({mx[0], mx[1], mx[2]}) << '\n';
}
signed main() {
std::cin.tie(nullptr)->sync_with_stdio(false);
int t;
std::cin >> t;
while (t -- ) {
solve();
}
return 0;
}
|
1003-Counting Stickmen
题目描述
给出一颗树,计算树中"火柴人"的个数。
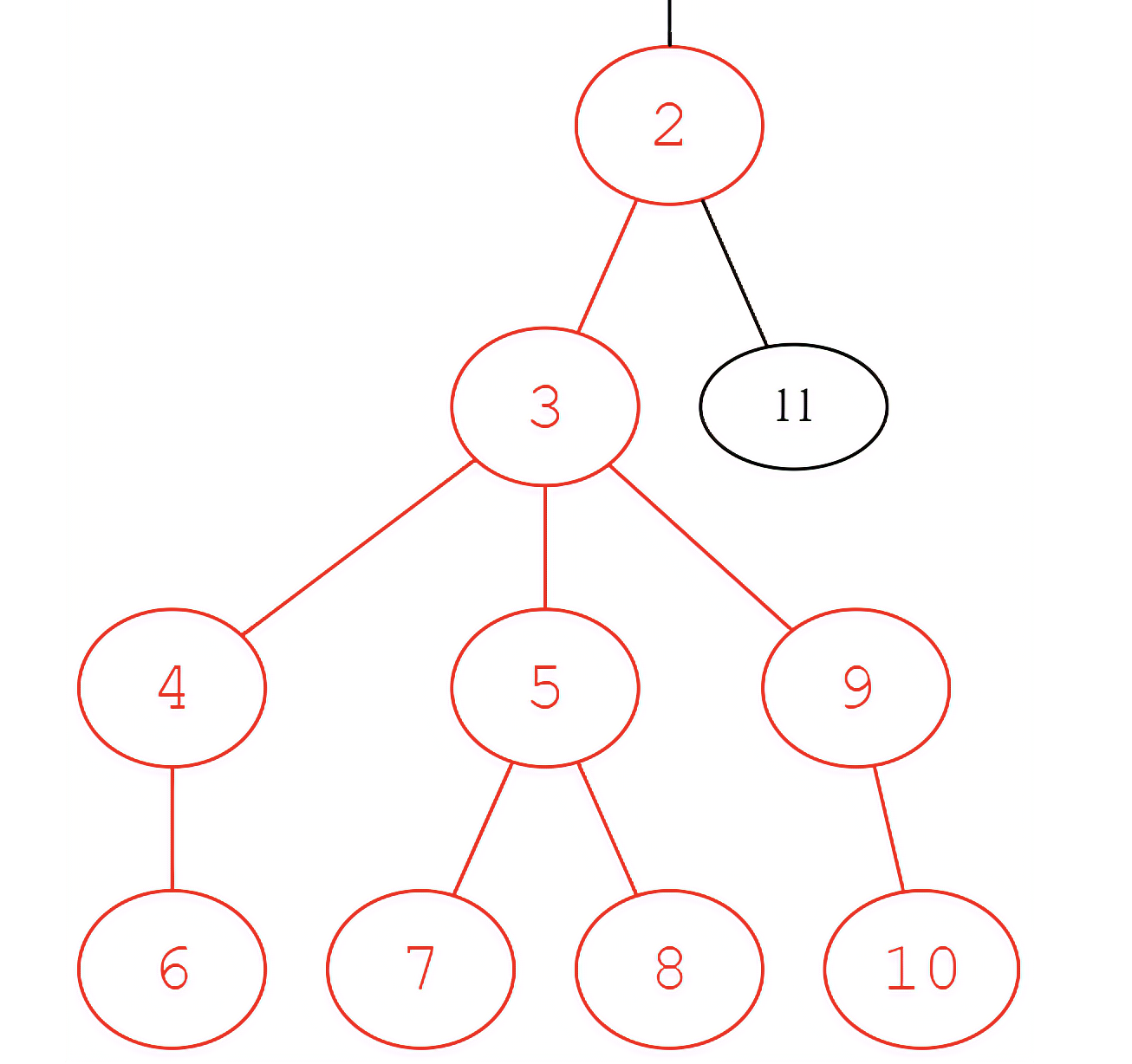
如图,$2$ 是火柴人的头,$(3,5)$ 是身子,$(4,6)(9,10)$ 是两条胳膊,$(5,7),(5,8)$ 是两条腿。
思路
我们暂且把它当做根节点为 $1$ 的树,枚举每个节点作为上图中 $3$ 位置的火柴人个数。
我们发现,火柴人的形态分为 $3$ 种。
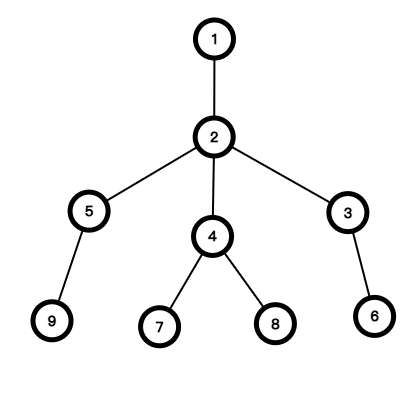
这种我称为正常形态。
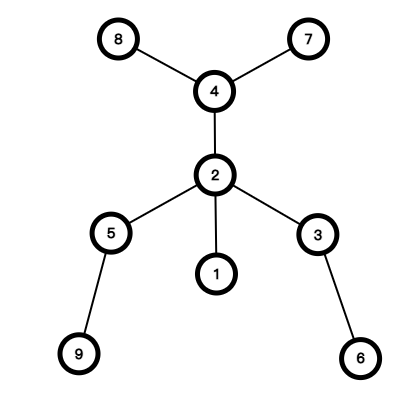
这种我称为头脚互换形态。
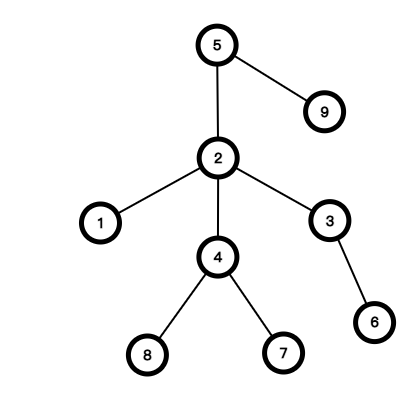
这种我称为头手互换形态。
然后对这三种形态分别计数即可。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
| #include<bits/stdc++.h>
using LL = long long;
const int N = 5e5 + 5, MOD = 998244353, INF = 0x3f3f3f3f;
int norm(int x) {
if (x < 0) {
x += MOD;
}
if (x >= MOD) {
x -= MOD;
}
return x;
}
template<class T>
T power(T a, LL b) {
T res = 1;
for (; b; b /= 2, a *= a) {
if (b % 2) {
res *= a;
}
}
return res;
}
struct Mint {
int x;
Mint(int x = 0) : x(norm(x)) {}
Mint(LL x) : x(norm(x % MOD)) {}
int val() const {
return x;
}
Mint operator-() const {
return Mint(norm(MOD - x));
}
Mint inv() const {
assert(x != 0);
return power(*this, MOD - 2);
}
Mint &operator*=(const Mint &rhs) {
x = LL(x) * rhs.x % MOD;
return *this;
}
Mint &operator+=(const Mint &rhs) {
x = norm(x + rhs.x);
return *this;
}
Mint &operator-=(const Mint &rhs) {
x = norm(x - rhs.x);
return *this;
}
Mint &operator/=(const Mint &rhs) {
return *this *= rhs.inv();
}
friend Mint operator*(const Mint &lhs, const Mint &rhs) {
Mint res = lhs;
res *= rhs;
return res;
}
friend Mint operator+(const Mint &lhs, const Mint &rhs) {
Mint res = lhs;
res += rhs;
return res;
}
friend Mint operator-(const Mint &lhs, const Mint &rhs) {
Mint res = lhs;
res -= rhs;
return res;
}
friend Mint operator/(const Mint &lhs, const Mint &rhs) {
Mint res = lhs;
res /= rhs;
return res;
}
friend std::istream &operator>>(std::istream &is, Mint &a) {
LL v;
is >> v;
a = Mint(v);
return is;
}
friend std::ostream &operator<<(std::ostream &os, const Mint &a) {
return os << a.val();
}
};
Mint inv[N], fac[N], finv[N];
void Pre_Work() {
fac[0] = fac[1] = 1;
inv[1] = 1;
finv[0] = finv[1] = 1;
for(int i = 2; i < N; ++ i) {
fac[i] = fac[i-1] * i;
inv[i] = MOD - MOD / i * inv[MOD % i];
finv[i] = finv[i - 1] * inv[i];
}
}
Mint C(int x, int y) {
if (x < y) {
return 0;
}
return fac[x] * finv[x - y] * finv[y];
}
std::vector< int > adj[N];
Mint ans[N];
int son[N], fa[N];
void dfs(int x, int p) {
fa[x] = p;
for (const auto &y : adj[x]) {
if (y ^ p) {
++ son[x];
dfs(y, x);
}
}
}
void dfs2(int x, int p) {
int cnt = 0;
fa[x] = p;
Mint siz = 0, all = 0;
for (const auto &y : adj[x]) {
if (y ^ p) {
dfs2(y, x);
if (son[y] >= 1) {
++ cnt;
}
siz += son[y];
}
}
if (son[x] >= 3) {
for (const auto &y : adj[x]) {
if (y ^ p) {
all += (Mint)(1LL * (siz - son[y]) * son[y]);
}
}
}
all /= 2;
if (son[x] >= 3) {
for (const auto &y : adj[x]) {
if (y ^ p) {
if (son[y] >= 2) {
ans[x] += (all - (son[y] * (siz - son[y]))) * C(son[y], 2) * C((fa[x] ? 1 : 0) + son[x] - 3, 1);
ans[x] += C(son[y], 2) * (siz - son[y]) * C(son[p] - 1 + (fa[p] ? 1 : 0), 1) * C(son[x] - 2, 1);
}
}
}
ans[x] += C(son[p] - 1 + (fa[p] ? 1 : 0), 2) * all * C(son[x] - 2, 1);
}
}
void solve() {
int n;
std::cin >> n;
for (int i = 0; i <= n; ++ i) {
adj[i].clear();
ans[i] = 0;
son[i] = fa[i] = 0;
}
for (int i = 1; i < n; ++ i) {
int u, v;
std::cin >> u >> v;
adj[u].push_back(v);
adj[v].push_back(u);
}
dfs(1, 0);
dfs2(1, 0);
Mint res = 0;
for (int i = 1; i <= n; ++ i) {
res += ans[i];
}
std::cout << res << '\n';
}
signed main() {
std::cin.tie(nullptr)->sync_with_stdio(false);
Pre_Work();
int t;
std::cin >> t;
while (t -- ) {
solve();
}
return 0;
}
|
1004-Black Magic
题目描述
我们定义每块砖都有左右两块区域,假设 $x$ 和 $y$ 是两块相邻的砖,若 $x$ 的右半边和 $y$ 的左边边都是黑色时,它俩就能合并为同一块。
给你 $E$ 块左右都为白色的砖,$L$ 块左边为黑色右边为白色的砖,$R$ 块右边为黑色左边为白色的砖,$B$ 块左右都为黑色的砖,求最终能得到的最少的砖块数和最多的砖块数。
思路
最少的情况很显然,就是左边为白右边为黑的和左边为黑右边为白的砖结合,然后把全黑的砖随便插在这俩中间。
最多的情况也很显然,就是左边摆 左黑右边,右边摆 左白右黑,中间将全黑和全白错排。
代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
| #include<bits/stdc++.h>
using LL = long long;
const int N = 2e5 + 5, MOD = 998244353, INF = 0x3f3f3f3f;
signed main() {
std::cin.tie(nullptr)->sync_with_stdio(false);
int t;
std::cin >> t;
while (t -- ) {
LL E, L, R, B;
std::cin >> E >> L >> R >> B;
LL ans_min = E + std::max(L, R) + (L == 0 && R == 0 ? B ? 1 : 0 : 0);
LL ans_max = L + R + (E >= B - 1 ? E + B : E * 2 + 1);
std::cout << ans_min << ' ' << ans_max << '\n';
}
return 0;
}
|
1006-Sumire
题目描述
我们定义 $f^k(B,x, d)$ 代表 $B$ 进制的 $x$ 中数字 $d$ 出现次数的 $k$ 次方。
给出 $k,B,d,l,r$ 求 $\sum_{i=l}^{r} f^{k}(B,i,d)$。
思路
一眼数位 $dp$ ,但是直接写会 $TLE$ ,我们观察到从 $0$ 到 $res$ 会计算很多重复的值,我们从这里为切入点来进行优化。
这里还是放官方题解的说法,感觉脑子想清楚了,但是嘴巴说不清楚。

于是赛中写了 $50$ 行的分类讨论,我称为分类讨论贵物,好在最后 $20min$ 过掉了。
代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
| #include<bits/stdc++.h>
using LL = long long;
const LL N = 100, MOD = 1e9 + 7, INF = 0x3f3f3f3f;
#define int LL
LL ksm(LL x, LL y, LL res = 1) {
if (x == 0) {
return 0;
}
if (y == 0) {
return 1;
}
for (; y; y >>= 1, x = x * x % MOD) {
if (y & 1) {
res = res * x % MOD;
}
}
return res;
}
std::vector< int > Trans(LL x, int b) {
std::vector< int > ans;
while (x) {
ans.push_back(x % b);
x /= b;
}
return ans;
}
int k, B, d, a[N], cnt;
LL dp[N][N][2][2];
LL dfs(int pos, int cnt, bool lead, bool limit) {
if (!pos) {
return ksm(cnt, k);
}
if (~dp[pos][cnt][lead][limit]) {
return dp[pos][cnt][lead][limit];
}
int res = limit ? a[pos] : B - 1;
LL ans = 0;
LL num = 0;
if (lead) {
bool flag = false;
ans += dfs(pos - 1, cnt, true, limit && (0 == a[pos]));
ans %= MOD;
if (0 == a[pos]) {
flag = true;
}
num += 1;
if (d != 0 && d <= res) {
ans += dfs(pos - 1, cnt + 1, false, limit && (d == a[pos]));
ans %= MOD;
if (d == a[pos]) {
flag = true;
}
num += 1;
}
if (flag) {
ans += (res + 1 - num) * dfs(pos - 1, cnt, false, false) % MOD;
ans %= MOD;
} else {
if (a[pos] <= res) {
ans += dfs(pos - 1, cnt, false, limit);
num += 1;
ans %= MOD;
}
ans += (res + 1 - num) * dfs(pos - 1, cnt, false, false) % MOD;
ans %= MOD;
}
} else {
bool flag = false;
if (d <= res) {
num += 1;
ans += dfs(pos - 1, cnt + 1, false, limit && (d == a[pos]));
ans %= MOD;
if (d == a[pos]) {
flag = true;
}
}
if (flag) {
ans += (res + 1 - num) * dfs(pos - 1, cnt, false, false);
ans %= MOD;
} else {
if (a[pos] <= res) {
ans += dfs(pos - 1, cnt, false, limit);
num += 1;
ans %= MOD;
}
ans += (res + 1 - num) * dfs(pos - 1, cnt, false, false) % MOD;
ans %= MOD;
}
}
return dp[pos][cnt][lead][limit] = (ans % MOD + MOD) % MOD;
}
LL calc(std::vector< int > x) {
cnt = 0;
for (int i = 0; i < x.size(); ++ i) {
a[++ cnt] = x[i];
}
memset(dp, -1, sizeof dp);
return dfs(cnt, 0, true, true);
}
void solve() {
LL l, r;
std::cin >> k >> B >> d >> l >> r;
-- l;
std::vector< int > L = Trans(l, B), R = Trans(r, B);
LL ans = (calc(R) - calc(L)) % MOD;
std::cout << (ans % MOD + MOD) % MOD << '\n';
}
signed main() {
std::cin.tie(nullptr)->sync_with_stdio(false);
int t;
std::cin >> t;
while (t -- ) {
solve();
}
return 0;
}
|
1008-Triangle Game
题目描述
给出三角形的三条边,每个回合都必须选择一条边减去一个正整数但是必须保证减去后还能构成一个三角形,不能操作者输掉比赛。
思路
受到昨天牛客多校的启发,每条边长度肯定要至少为 $1$ ,异或和不为 $0$ 则先手赢。
证明还是得看官方题解

代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
| #include<bits/stdc++.h>
using LL = long long;
const int N = 2e5 + 5, MOD = 998244353, INF = 0x3f3f3f3f;
signed main() {
std::cin.tie(nullptr)->sync_with_stdio(false);
int t;
std::cin >> t;
while (t -- ) {
int a, b, c;
std::cin >> a >> b >> c;
-- a;
-- b;
-- c;
std::cout << ((a ^ b ^ c) == 0 ? "Lose" : "Win") << '\n';
}
return 0;
}
|