1006-Maex

题目描述

给出以$1$为根的树，你可以给每个点赋不同的值，我们定义该点的贡献为以这个点为根节点的子树内的$MEX$（最小未出现过的数），求所有节点贡献和的最大值。

思路

$dp_x$代表以$x$为根节点的子树最大贡献和。

代码

#include<bits/stdc++.h>
using namespace std;
using LL = long long;
const int N = 5e5 + 5, MOD = 998244353, INF = 0x3f3f3f3f;

int n;
vector< int > adj[N];
int num, siz[N];
LL dp[N];
void dfs(int x, int p) {
    siz[x] = 1;
    for (auto &y : adj[x]) {
        if (y ^ p) {
            dfs(y, x);
            siz[x] += siz[y];
            dp[x] = max(dp[x], dp[y]);
        }
    }
    dp[x] += siz[x];
}
void solve() {
    cin >> n;
    for (int i = 1; i <= n; ++ i) {
        adj[i].clear();
        siz[i] = dp[i] = 0;
    }
    for (int i = 1; i < n; ++ i) {
        int u, v;
        cin >> u >> v;
        adj[u].push_back(v);
        adj[v].push_back(u);
    }
    dfs(1, 0);
    cout << dp[1] << '\n';
}
signed main() {
    cin.tie(nullptr)->sync_with_stdio(false);

    int t;
    cin >> t;
    while (t -- ) {
        solve();
    }
    return 0;
}

1007-Shinobu loves trip

题目描述

有$n$条旅游路线，每条路线有一个起点$s$以及旅行天数$d$，一开始在起点，第$i$天在$s + a \times d \mod p$。

$q$次询问，每次询问有多少条路线会经过$x$。

思路

若第 $i$ 条路线经过 $x$ ，那么满足 $s_i + a^k \mod p \equiv x$，移项得 $a^k \mod p \equiv \frac {x}{s_i} \mod p$。也就是说存在 $0 \leq k \leq d_i$ 满足前面的等式。

我们可以预处理出 $a^i \mod p$ 最先出现的 $i$，然后查询时我们对每一条路线询问 $\frac{x}{s_i} \mod p$ 最早出现时间是否 $\leq d_i$。

注意，若起点为 $0$ 的话，整条路线都是重复在走 $0$ 这个点，所以我们要特判一下。

代码

#include <iostream>
#include <unordered_map>
using namespace std;
using LL = long long;
const int N = 1005, MOD = 998244353, INF = 0x3f3f3f3f;

int p, a, n, q;
int s[N], d[N], inv[N];
LL ksm(LL x, LL y, LL P) {
    LL res = 1;
    for (; y; y >>= 1, x = x * x % P) {
        if (y & 1) {
            res = res * x % P;
        }
    }
    return res;
}
void solve() {
    cin >> p >> a >> n >> q;
    unordered_map< int, int > fir;
    for (int i = 1, x = 1; i <= 200005; ++ i, x = (LL)x * a % p) {
        if (!fir[x]) {
            fir[x] = i;
        }
    }
    for (int i = 1; i <= n; ++ i) {
        cin >> s[i] >> d[i];
        ++ d[i];
        inv[i] = ksm(s[i], p - 2, p);
    }

    while (q -- ) {
        int x, ans = 0;
        cin >> x;
        if( x == 0 ) {
            for (int i = 1; i <= n; ++ i) {
                if( s[i] == 0 ) ++ ans;
            }
        }
        else {
            for (int i = 1; i <= n; ++ i) {
                int pos = (LL)x * inv[i] % p;
                if (fir[pos] && fir[pos] <= d[i]) {
                    ++ ans;
                }
            }
        }
        cout << ans << '\n';
        // cout << '\n';
    }
}
signed main() {
    cin.tie(nullptr)->sync_with_stdio(false);

    int t;
    cin >> t;
    while (t -- ) {
        solve();
    }
    return 0;
}

/*
2
3 2 1 1
1 1
2
5 4 3 3
1 4
4 3
0 100
4
2
0

*/

1010-Planar graph

题目描述

给出一张平面图，求用数量最少且编号最小的边使不同平面之间能够连通。

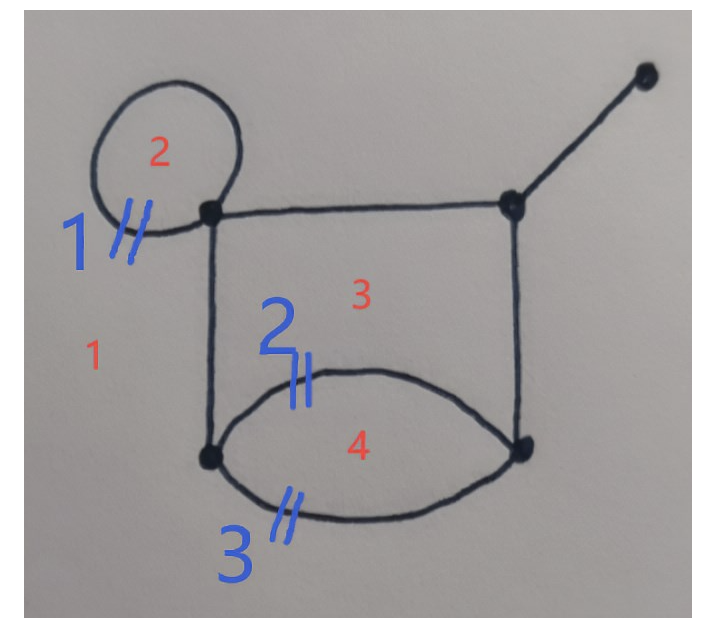
graph1

比如这张图就把整个平面分割成了 $4$ 个部分，使用编号为 $1、2、3$ 的边能够让这 $4$ 个部分连通。

思路

首先分割平面的条件为产生闭环，手玩几个样例之后我们会发现其实答案的个数其实是固定的，就是分割的平面的个数减一，是不是很像 $Kruskal$ ？因为要求边的编号最小，所以我们可以倒着加边，当两个端点在连接之前就已经在一块了，那么这时就产生了闭环，说明新的平面要产生了，这时这条边就是当前的最优边，然后重复这个过程。

很像吐槽的是，$hdu$ 的评测机居然会把 $RE$ 判成 $WA$，让我以为我想错了，结果数组开大一倍就过了…

代码

#include<bits/stdc++.h>
using namespace std;
using LL = long long;
const int N = 1e5 + 5, MOD = 998244353, INF = 0x3f3f3f3f;

int n, m, f[N], u[N * 2], v[N * 2];
int find(int x) {
    return f[x] == x ? x : f[x] = find(f[x]);
}
void solve() {
    cin >> n >> m;
    for (int i = 1; i <= m; ++ i) {
        cin >> u[i] >> v[i];
    }
    for (int i = 1; i <= n; ++ i) {
        f[i] = i;
    }
    vector< int > idx;
    for (int i = m; i >= 1; -- i) {
        int fx = find(u[i]), fy = find(v[i]);
        if (fx == fy) {
            idx.push_back(i);
        } else {
            f[fx] = fy;
        }
    }
    cout << idx.size() << '\n';
    sort(idx.begin(), idx.end());
    for (auto &x : idx) {
        cout << x << ' ';
    }
    cout << '\n';
}
signed main() {
    cin.tie(nullptr)->sync_with_stdio(false);

    int t;
    cin >> t;
    while (t -- ) {
        solve();
    }
    return 0;
}

1012-Loop

题目描述

给出一个长度为 $n$ 的序列，你可以进行 $k$ 次操作，每次操作你都可以选择一个区间 $[l,r]$，让 $a_{i+1}=a_i(l \leq i \leq r-1)$，然后让 $a_l$ 等于原来的 $a_r$。

求$k$次操作后，字典序最大的序列是多少。

思路

首先，我们考虑什么时候应该将 $a_i$ 挪到后面去，当后面有 $a_j$ 大于 $a_i$ 并且 $a_i$ 是前面小于 $a_j$ 的数里最小的数，这时我们就可以将 $a_i$ 挪到后面，然后将 $k$ 减 $1$。我们先不管将这些数挪到哪里，先将它们存起来。

当 $k$ 减到 $0$ 时，我们考虑将之前存起来的数插到剩余序列里去，我们贪心地将它们从大到小地插入。

我们考虑什么时候插入是最优的，设剩余的数组成的序列为 $b$ ，拿出来的数里当前最大的数为 $x$ ，当 $b_i \ge x >b_{i+1}$ 时我们将 $x$ 插入到 $b_i$ 和 $b_{i+1}$ 之间是最优的。

代码

#include<bits/stdc++.h>
using namespace std;
using LL = long long;
const int N = 3e5 + 5, MOD = 998244353, INF = 0x3f3f3f3f;

int n, k, a[N];
bool vis[N];
void solve() {
    cin >> n >> k;
    set< pair< int, int > > st;
    for (int i = 1; i <= n; ++ i) {
        vis[i] = false;
    }
    vector< int > a1, a2;
    for (int i = 1; i <= n; ++ i) {
        cin >> a[i];
        while (k && !st.empty() && st.begin()->first < a[i]) {
            vis[st.begin()->second] = true;
            a2.push_back(st.begin()->first);
            st.erase(st.begin());
            -- k;
        }
        st.insert({a[i], i});
    }
    while (k && !st.empty()) {
        vis[st.begin()->second] = true;
        a2.push_back(st.begin()->first);
        st.erase(st.begin());
        -- k;
    }
    sort(a2.begin(), a2.end());
    for (int i = 1; i <= n; ++ i) {
        if (!vis[i]) {
            a1.push_back(a[i]);
        }
    }
    vector< int > ans;
    for (int i = 0; i < a1.size(); ++ i) {
        ans.push_back(a1[i]);
        if (i + 1 < a1.size()) {
            while (!a2.empty() && a1[i] >= a2.back() && a2.back() > a1[i + 1]) {
                ans.push_back(a2.back());
                a2.pop_back();
            }
        }
    }
    while (!a2.empty()) {
        ans.push_back(a2.back());
        a2.pop_back();
    }
    for (int i = 0; i < ans.size(); ++ i) {
        cout << ans[i] << " \n"[i + 1 == ans.size()];
    }
}
signed main() {
    cin.tie(nullptr)->sync_with_stdio(false);

    int t;
    cin >> t;
    while (t -- ) {
        solve();
    }    
    return 0;
}